Determination of bolt forces from shear loads
- kamilmaruszakuk
- Jul 30, 2018
- 3 min read
Updated: Oct 8, 2020
It is not difficult to derive bolt forces from a single vertical load or a horizontal load acting on the specific number of bolts. What is more difficult, however is the determination of forces acting on a single bolt from a torsional moment, especially in combination with other loads. In this article we are going to explain how to find a resultant force from loads acting on a bolt in different directions.
Let us consider an end plate connection with 6 bolts, as shown in Figure 1. We can put any number of bolts if we want to (n-value).

Figure 1.
The figures below (Figure 2 and Figure 3) illustrate the distribution of forces for a vertical shear load and a horizontal shear load, respectively. It is important to make sure that these loads are applied in the centroid of the bolts. If not, an additional moment due to force eccentricity will have to be added to the torsional moment, which will be discussed later.

Figure 2.

Figure 3.
First thing to consider when dealing with a torsional moment is to derive the centroid of bolts – point 0 in figures above. If there is a torsional moment with vertical and horizontal loads applied eccentrically, the total torsional moment will now equal to:
Mx = Mt+V•y+H•z
The next step is to determine the forces, on each bolt, from the total torsional moment. In our case the end plate is assumed to be rigid, compared to the stiffness of fasteners. When there are small deformations of the bolts, a linear relationship between the bolt forces and the displacement may be assumed. This means that bolt forces are proportional to the distance from the centre of rotation, thus centroid of bolts in our case, this is known as a free centre of rotation. Figure 4 below shows how the torsional moment is replaced with shear forces acting on the bolts. Forces in yellow are always perpendicular to the line between the point 0 and the bolt being considered.

Figure 4.
Two lower bolts have the highest value of forces acting on them. This is due to these bolts having the longest distance from point 0. The exact values may be derived from the formula below:

where Mx is the total torsional moment;
rmax - is the distance to the bolt considered and
ri – is the distance to other bolts.
The final step is to combine all loads and find a final resultant force. Figure 5 shows one bolt with forces from the vertical load (Fv,1), the horizontal load (Fh,1) and the torsional moment (Fm,1).
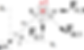
Figure 5.
The force from the torsional moment will have to be resolved in the y-direction and in the z-direction. To do so we have to use some trigonometric rules, keeping in mind the right angle between the FM,1 force and r01 distance. Adding a vertical component of Fm,1 force to the vertical shear force FV,1 and , similarly, adding a horizontal component of Fm,1 force to the horizontal shear force Fh,1 will give us the sum of two different forces in two directions. The last thing is to combine these two forces using Pythagoras’s theorem and we will get the final resultant force acting on the bolt. The resistance of the considered bolt in shear will have to be bigger than the derived force. It should be noted that some bolts might be also subject to combined shear and tension, thus the total resistance will have to be reduced accordingly.


























